ANR HIWAI

Inversion homogénéisée de formes d’ondes sismiques

Depuis l’échelle de quelques mètres à celle de la Terre globale, l’imagerie sismique est un outil de choix pour étudier l’intérieur de la terre pour des objectifs industriels et académiques. Récemment, les techniques basées sur l’inversion des formes d’ondes (IFO) générées par des sources actives (airgun) ou passives (tremblement de Terre) ont fait d’importants progrès, à tel point que ces méthodes sont maintenant crédibles pour des applications à des cas réels d’imageries 3-D de structures géologiques. Ce domaine est très actif et compétitif au niveau international, à la fois dans les mondes académiques et industriels. Cependant, ces méthodes représentent toujours des défis techniques et théoriques très importants. Actuellement, elles sont basées sur une approche de type moindre carré linéarisée et stabilisée et sont mises en difficultés dans les cas de fonction coût avec des minimums locaux multiples et de non unicité de la solution, ce qui est souvent le cas pour des milieux fortement contrastés. De plus l’interprétation des modèles obtenus, l’estimation des incertitudes mais aussi le coût calcul limitent fortement les possibilités d’applications de ces méthodes.

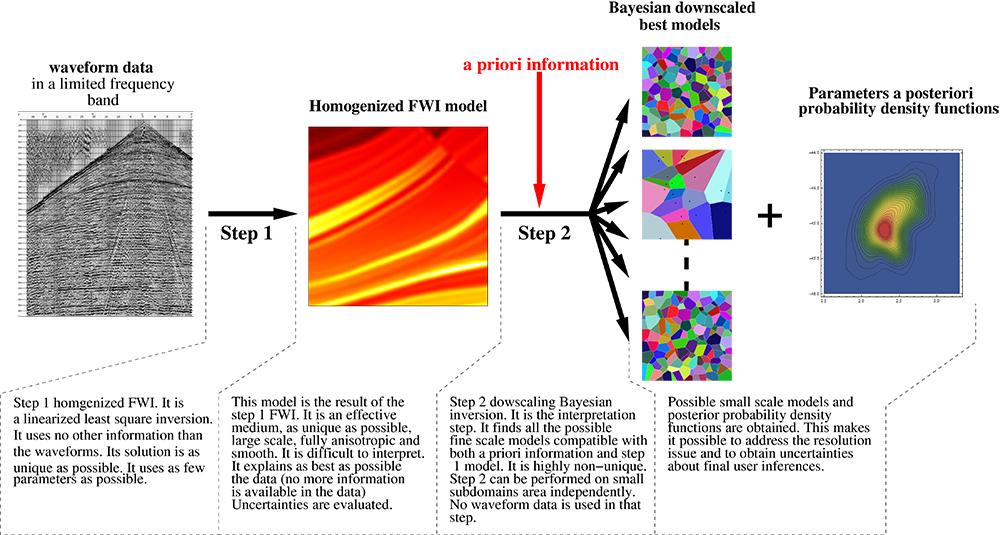
**Schéma synthétique du principe du projet HIWAI**

L’objectif principal d’HIWAI est, grâce une nouvelle approche innovante basée sur les outils d’homogénéisation non périodique et d’inversion Bayésienne, de largement étendre le domaine d’application de l’IFO et ainsi de permettre des applications intéressantes d’un point vue scientifique et sociétal, jusqu’alors inaccessibles. Une méthode à 2 étapes, permettant de s’approcher d’une solution complètement Bayésienne de ce problème inverse (solution qui est considérée comme inaccessible avec les puissances de calculs actuelles) sera développée. En cas de succès, ce développement représenterait une percée importante.

Parmi les applications possibles d’un tel développement, l’imagerie des milieux élastiques fortement contrastés qui mettent souvent en échec les méthodes actuelles, est particulièrement intéressante. Ce type de milieux se trouve souvent aux échelles géotechniques, pour la prévention des risques naturels, comme pour l’imagerie de fondations, la détection de cavités souterraines, ou bien, dans le cas de l’exploration pétrolière, pour l’étude de réservoirs complexes. Par ailleurs, les modèles obtenus seront particulièrement adaptés à des prédictions de qualité de données sismiques, nécessaires par exemple pour la surveillance des essais nucléaires ou l’étude du risque sismique. Un autre type d’applications important visé par ce projet est le cas où des informations qualitatives avec incertitudes sont nécessaires (par exemple: quelle est la probabilité de trouver une haute contenance en eau à telle profondeur?). Une autre application de ce type est la caractérisation de failles à l’échelle des réservoirs. Même si ces développements peuvent s’appliquer à toutes les échelles, les petites échelles, où les bénéfices du projet sont les plus prometteurs, seront particulièrement visées et testées.

**Principe d’homogénéisation**. On souhaite propager des ondes jusqu’à une fréquence maximale donnée dans un modèle élastique complexe (a) utilisant un solveur numérique (par exemple la méthode des éléments spectraux). La première solution classique consiste à mailler toutes les discontinuités de (a) pour obtenir le maillage complexe (b) (ici un maillage d’éléments spectraux) puis pour effectuer la modélisation de la forme d’onde (1) pour obtenir le champ d’onde (e). La deuxième option consiste à utiliser l’homogénéisation pour calculer l’efficacité du modèle élastique (c) de (a). (c) est entièrement anisotrope mais lisse, ce qui conduit à un maillage simple (d). Enfin la forme d’onde de la modélisation (2) est effectuée avec le même solveur numérique que celui utilisé pour la modélisation de la forme d’onde (1) pour obtenir champ d’onde (f), mais à un niveau numérique inférieur à (e). Pour un modèle homogénéisation suffisamment détaillé, (f) converge vers (e). Pour une perspective d’inversion, la recherche du modèle homogénéisé est une tâche beaucoup plus simple que la recherche du modèle original.

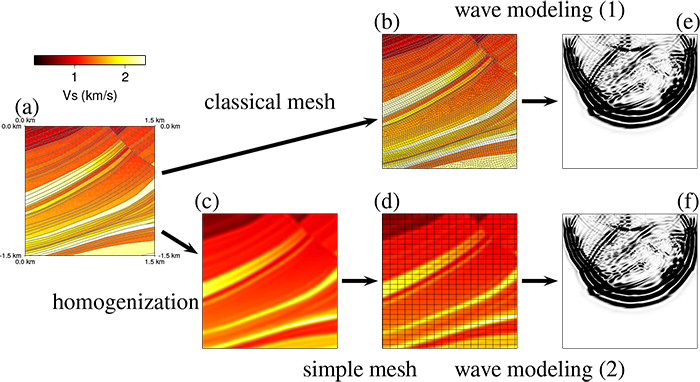
Le projet s’organise en 4 tâches : 1) développements à 2-D de l’IFO homogénéisée (étape 1), 2) inversion Bayésienne d’interprétation (étape 2), 3) génération de données de modèles réduits pour tester les inversions, 4) développements 3-D. Grâce à un projet de type collaboratif (instrument PRC), toutes les compétences nécessaires au succès du projet seront rassemblées avec 5 partenaires: homogénéisation et inversion (LPGNantes), inversion sismique à l’échelle de l’exploration (SEISCOPE2, Grenoble), données de modèles réduits et imagerie sub-surface (IFSTTAR, Bouguenais), inversion Bayésienne (ENS Lyon) et génération de géomodèles (RING, Nancy). Ce projet fournira un cadre de recherche au long terme pour les différentes équipes impliquées et, dans un futur proche, des partenaires industriels seront impliqués pour s’attaquer à des applications pratiques.

Le coordinateur du projet est Yann Capdeville, Directeur de Recherche CNRS.